
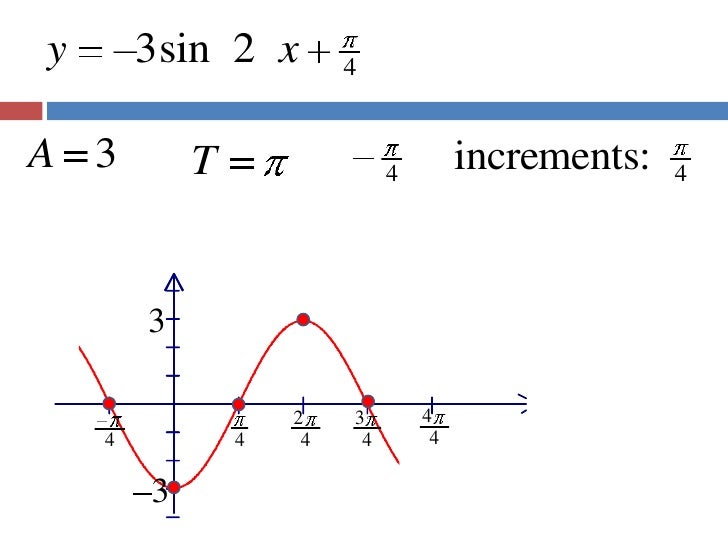
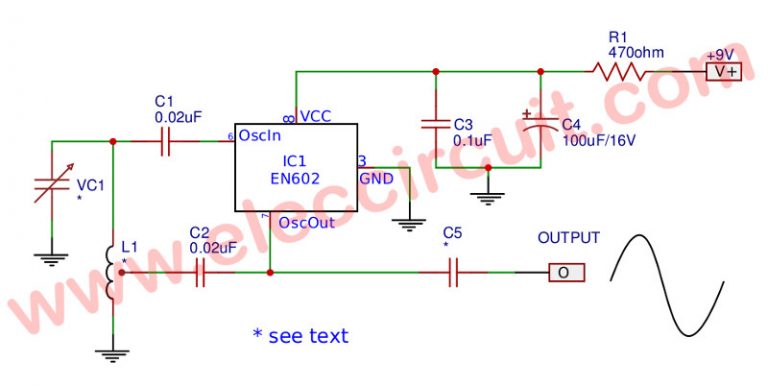
SINE FUNCTION EQUATION MAKER CODE
This code uses below C-wrapper to calculate forward 3D FFTW sine transform and backward 3D FFTW sine transform, #include Subroutine Backward_FFT(Nx, Ny, Nz, in, out)
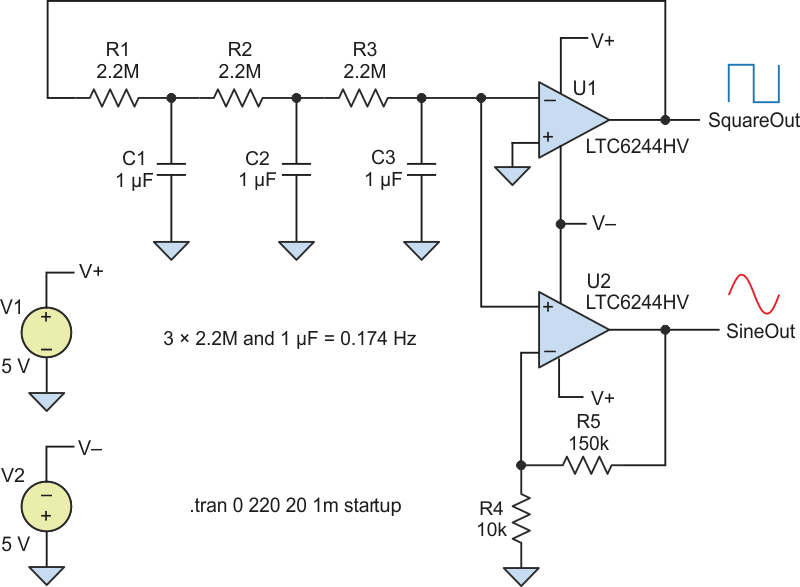
! Wrapper Subroutine to call backward fftw c functions for 3d arrays ! Real ( kind = 8 ) in(Nx, Ny, Nz),out(Nx, Ny, Nz),dum(Nx*Ny*Nz) Subroutine Forward_FFT(Nx, Ny, Nz, in, out) ! Wrapper Subroutine to call forward fftw c functions for 3d arrays ! ! = 3D DST =Ĭall Forward_FFT(Nx, Ny, Nz, in_dst, in_k_dst) Out_k_dft(i,j,k) = in_k_dft(i,j,k)/(kx*kx+ky*ky+kz*kz)Ĭall dfftw_plan_dft_c2r_3d_ (plan_backward, Nx, Ny, Nz, out_k_dft, out_dft, FFTW_ESTIMATE) ! = 3D DFT =Ĭall dfftw_plan_dft_r2c_3d_ (plan_forward, Nx, Ny, Nz, in_dft, in_k_dft, FFTW_ESTIMATE) Integer ( kind = 8 ) plan_forward,plan_backward ! DFT Real ( kind = 8 ) in_k_dst(Nx,Ny,Nz),out_k_dst(Nx,Ny,Nz) ! DST Real ( kind = 8 ) in_dst(Nx,Ny,Nz),out_dst(Nx,Ny,Nz) ! DST Real ( kind = 8 ) Lx,Ly,Lz,dx,dy,dz,kx,ky,kz Integer ( kind = 4 ), parameter :: Nz = 64 Integer ( kind = 4 ), parameter :: Ny = 64 Integer ( kind = 4 ), parameter :: Nx = 64 ! To run this code: gcc dst_3d.c -c -std=c99 & gfortran derivative.f95 dst_3d.o -lfftw3 &. This says my code for Poisson equation solver works fine in case of normal FFTW. Then inverse FFTW of c2r (complex to real) type regenerates the input function but the amplitude now reduced to 1 as shown in 3-D plot 2. amplitude along z-axis against x-,y- co-ordinate. A 3-D plot of amplitude of input function shows it's correct amplitude. r2c (real to complex) type of a mathematical function 27*sin(3x)*sin(3y)*sin(3z) and then divide it by 27 (3*3+3*3+3*3) to calculate second derivative of input function. In this code, first I have done normal FFTW i.e. I have written following code in Fortran to solve Poisson's equation using r2r (real to real) type FFTW sin transform.


 0 kommentar(er)
0 kommentar(er)
